一 什么是AVL树(平衡二叉树):
AVL树本质上是一颗二叉查找树,但是它又具有以下特点:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。在AVL树中任何节点的两个子树的高度最大差别为一,所以它也被称为平衡二叉树。下面是平衡二叉树和非平衡二叉树对比的例图:
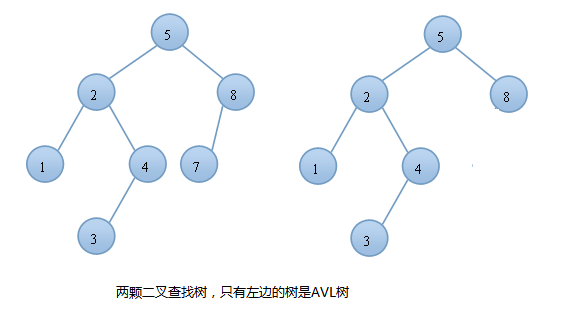
平衡因子(bf):结点的左子树的深度减去右子树的深度,那么显然-1<=bf<=1;
AVL树具有以下性质:
- 根的左右子树的高度之差的绝对值不能超过1
- 根的左右子树都是平衡二叉树
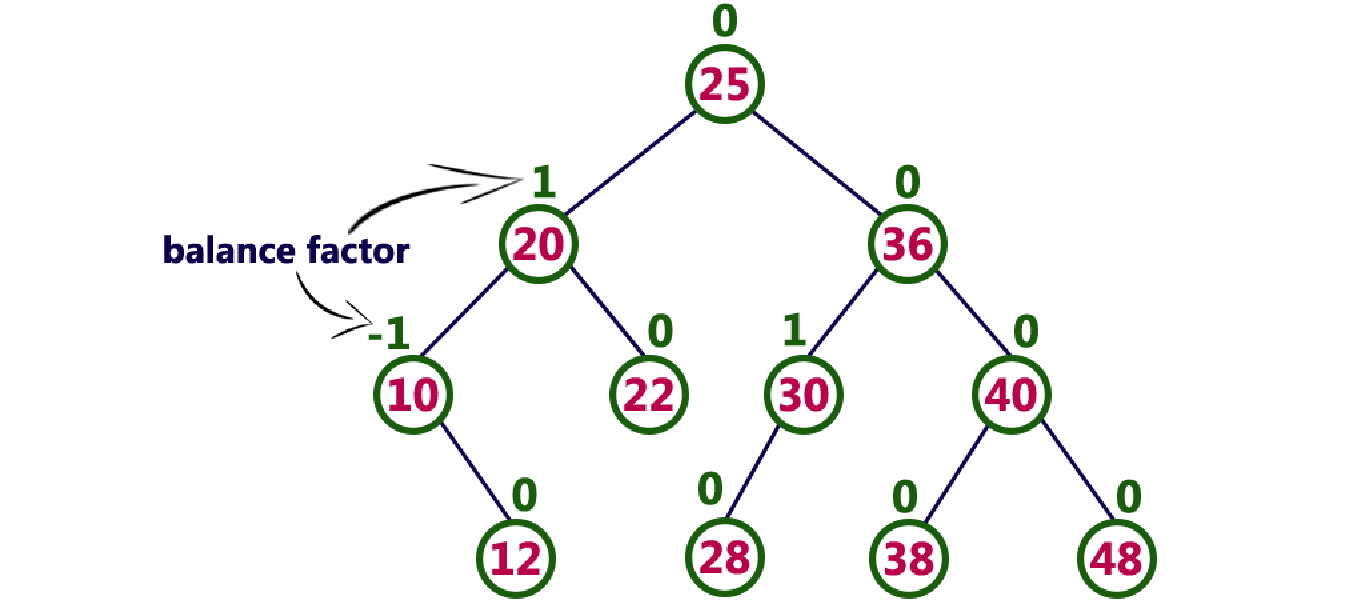
二 AVL树的旋转
插入一个节点可能会破坏AVL树的平衡, 可以通过旋转操作来进行修正
插入一个节点后,只有从插入节点到根节点的路径上的节点的平衡可能被改变。我们需要找出第一个破坏了平衡条件的节点,称之为K。K的两颗子树高度相差2 不平衡的出可能有4种情况:- 不平衡是由于对k的右孩子的右子树插入导致的:左旋
- 不平衡是由于对k的左孩子的左子树插入导致的:右旋
- 不平衡是由于对k的右孩子的左子树插入导致的:右旋-左旋
- 不平衡是由于对k的左孩子的右子树插入导致的:左旋-右旋
1 左旋
我们在进行节点插入的时候,可能会出现节点都倾向于左边的情况,例如:
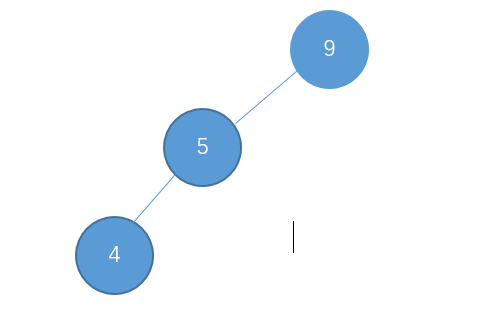
这个时候,我们就可以对节点9进行右旋操作,使它恢复平衡。
即:顺时针旋转两个节点,使得父节点被自己的左孩子取代,而自己成为自己的右孩子
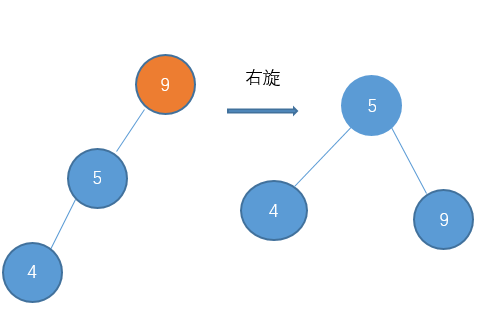
再举个例子:
节点4和9高度相差大于1。由于是左孩子的高度较高,此时是左-左型,进行右旋。
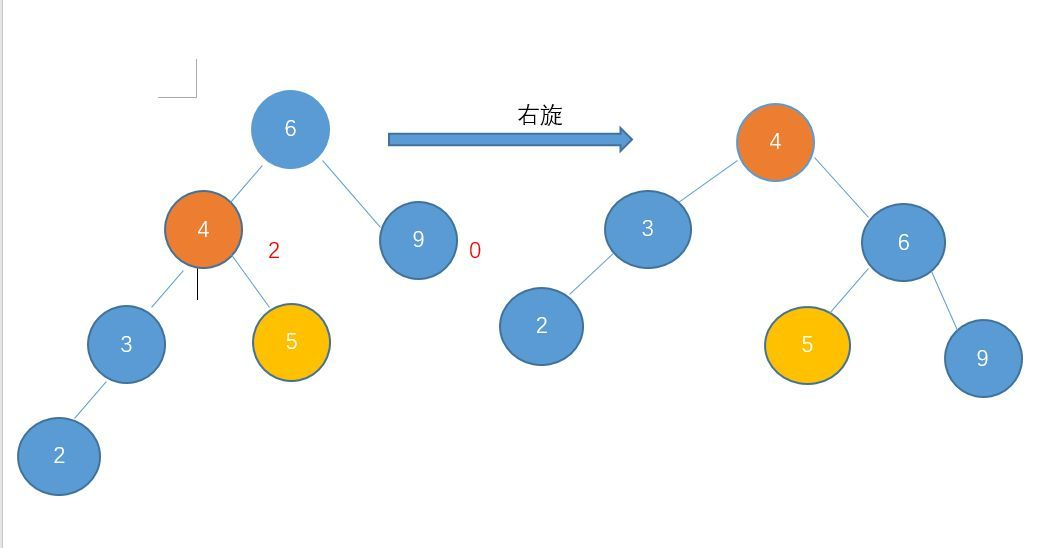
2 左旋
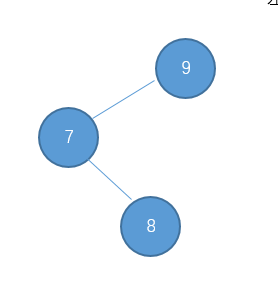
左旋和右旋一样,就是用来解决当大部分节点都偏向右边的时候,通过左旋来还原。例如:
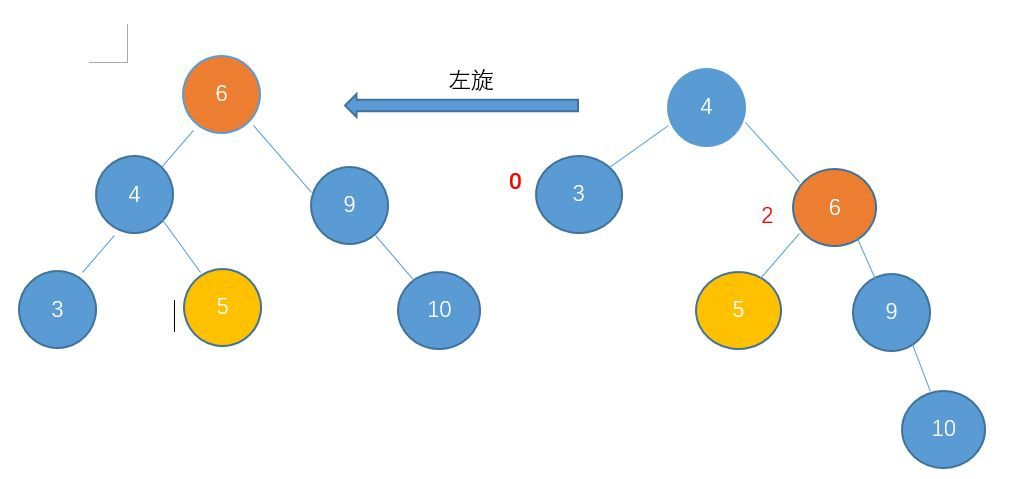
3 右旋左旋
对于图中画圈部分
单单一次左旋或右旋是不行的,下面我们先说说如何处理这种情况。
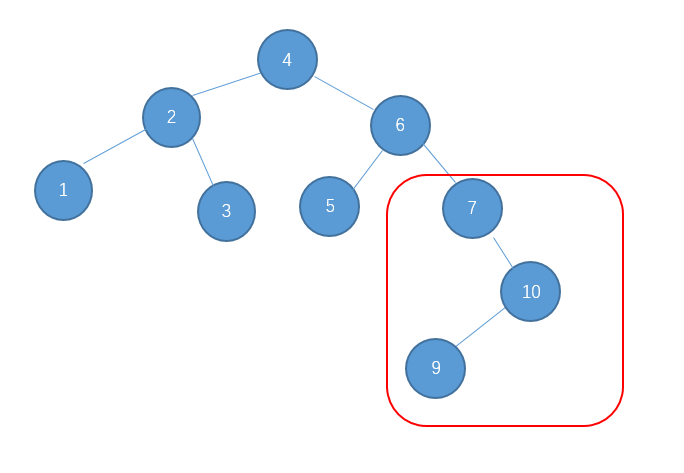
处理的方法是先对节点10进行右旋把它变成右-右型。
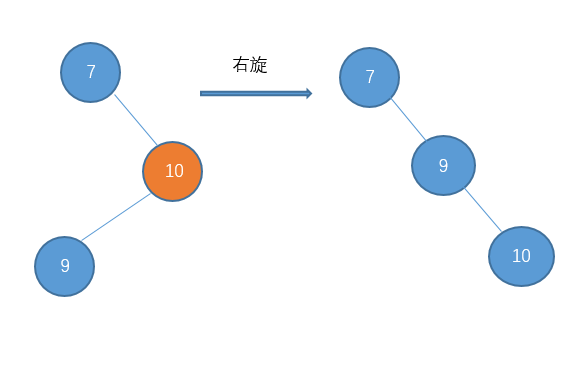
然后在进行左旋。
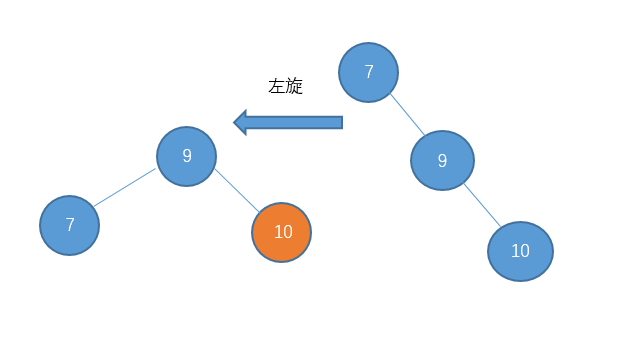
调整之后:

4 左旋右旋
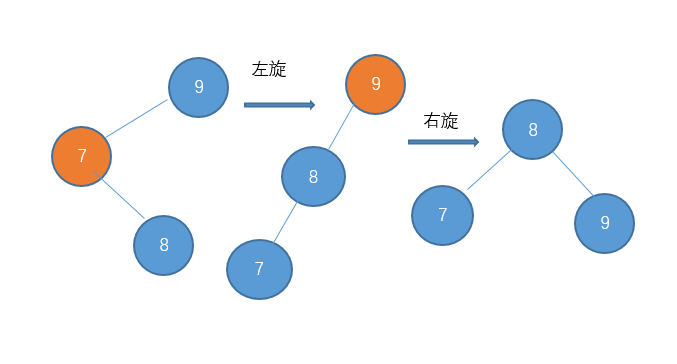
同理,也存在左-右型的,例如:
对于左-右型的情况和刚才的 右-左型相反,我们需要对它进行一次左旋,再右旋。
在插入的过程中,会出现一下四种情况破坏AVL树的特性,我们可以采取如下相应的旋转。
1、左-左型:做右旋。
2、右-右型:做左旋转。
3、左-右型:先做左旋,后做右旋。
4、右-左型:先做右旋,再做左旋。
三 AVL树的实现代码
1 class AVLNode(object): 2 def __init__(self, data): 3 ''' 4 AVL树的每个节点 5 ''' 6 7 self.data = data 8 self.lchild = None 9 self.rchild = None 10 self.parent = None 11 self.bf = 0 12 13 14 class AVLTree(object): 15 ''' 16 AVL树相关操作 17 ''' 18 19 def __init__(self, li=None): 20 self.root = None 21 if li: 22 for val in li: 23 self.insert_no_rec(val) 24 25 def pre_order(self, root): 26 if root: 27 print(root.data, end=",") 28 self.pre_order(root.lchild) 29 self.pre_order(root.rchild) 30 31 def in_order(self, root): 32 if root: 33 self.in_order(root.lchild) 34 print(root.data, end=',') 35 self.in_order(root.rchild) 36 37 def rotate_left(self, p, c): 38 s2 = c.lchild 39 p.rchild = s2 40 if s2: 41 s2.parent = p 42 c.lchild = p 43 p.parent = c 44 p.bf = 0 45 c.bf = 0 46 return c 47 48 def rotate_right(self, p, c): 49 s2 = c.rchild 50 p.lchild = s2 51 if s2: 52 s2.parent = p 53 c.rchild = p 54 p.parent = c 55 p.bf = 0 56 c.bf = 0 57 return c 58 59 def rotate_right_left(self, p, c): 60 g = c.lchild 61 s3 = g.rchild 62 c.lchild = s3 63 if s3: 64 s3.parent = c 65 g.rchild = c 66 c.parent = g 67 68 s2 = g.lchild 69 p.rchild = s2 70 if s2: 71 s2.parent = p 72 g.lchild = p 73 p.parent = g 74 75 # 更新bf 76 if g.bf > 0: 77 p.bf = -1 78 c.bf = 0 79 elif g.bf < 0: 80 p.bf = 0 81 c.bf = 1 82 else: # 插入的是g 83 p.bf = 0 84 c.bf = 0 85 return g 86 87 def rotate_left_right(self, p, c): 88 g = c.rchild 89 s2 = g.lchild 90 c.rchild = s2 91 if s2: 92 s2.parent = c 93 g.lchild = c 94 c.parent = g 95 96 s3 = g.rchild 97 p.lchild = s3 98 if s3: 99 s3.parent = p100 g.rchild = p101 p.parent = g102 103 # 更新bf104 if g.bf < 0:105 p.bf = 1106 c.bf = 0107 elif g.bf > 0:108 p.bf = 0109 c.bf = -1110 else:111 p.bf = 0112 c.bf = 0113 return g114 115 def insert_no_rec(self, val):116 # 1 和BST一样插入117 p = self.root118 if not p: # 空树119 self.root = AVLNode(val)120 return121 while True:122 if val < p.data:123 if p.lchild:124 p = p.lchild125 else: # 左子树不存在直接插入126 p.lchild = AVLNode(val)127 p.lchild.parent = p128 node = p.lchild # node存储就是插入的节点129 break130 elif val > p.data:131 if p.rchild:132 p = p.rchild133 else:134 p.rchild = AVLNode(val)135 p.rchild.parent = p136 node = p.rchild137 break138 else: # val == p.data 一颗树如果插入同样的元素 不操作139 return140 # 更新balance factor141 while node.parent: # node的parent不空142 if node.parent.lchild == node: # 传递是从左子树来的, 左子树更沉了143 # 更新node.parent的bf -=1144 if node.parent.bf < 0: # 原来node.parent.bf == -1, 更新后变成-2145 # 看node哪边沉146 g = node.parent.parent # 为了连接旋转之后的子树147 x = node.parent # 旋转之前子树的根148 if node.bf > 0:149 n = self.rotate_left_right(node.parent, node)150 else:151 n = self.rotate_right(node.parent, node)152 elif node.parent.bf > 0: # 原来node.parent.bf=1 更新之后变成0153 node.parent.bf = 0154 break155 else: # 原来node.parent.bf=0 更新之后变成-1156 node.parent.bf = -1157 node = node.parent158 continue159 else: # 传递是从右子树来的, 右子树更沉了160 # 更新node.parent.bf += 1161 if node.parent.bf > 0: # 原来node.parent.bf ==1, 更新后变成2162 # 做旋转163 # 看node那边沉164 g = node.parent.parent # 为了连接旋转之后的子树165 x = node.parent # 旋转之前子树的根166 if node.bf < 0: # node.bf = 1167 n = self.rotate_left_right(node.parent, node)168 else: # node.bf = -1169 n = self.rotate_left(node.parent, node)170 171 elif node.parent.bf < 0: # 原来node.parent.bf = -1 更新后变成0172 node.parent.bf = 0173 break174 else: # 原来node.parent.bf =0 更新之后变成1175 node.parent.bf = 1176 node = node.parent177 continue178 # 链接旋转后的子树179 n.parent = g180 if g: # g不是空181 if x == g.lchild:182 g.lchild = n183 else:184 g.rchild = n185 break186 else:187 self.root = n188 break189 190 191 tree = AVLTree([9, 8, 7, 6, 5, 4, 3, 2, 1])192 tree.pre_order(tree.root)193 print("")194 tree.in_order(tree.root)